二叉树是一种非常重要的数据结构,可以视为一种介于图和链表之间的半线性数据结构,或者视为一种特殊的图。因此对于二叉树,有深度优先遍历和广度优先遍历,深度优先遍历有前序、中序以及后序三种遍历方法,而广度优先遍历即是层序遍历,一次遍历二叉树每一层节点。因为树的定义本身就是递归定义,因此采用递归的方法去实现树的三种深度优先遍历不仅容易理解而且代码很简洁,而递归本身是操作系统内部实现了栈结构来实现,因此我们可以通过自己构造栈结构来将递归实现转化为迭代实现。而对于广度优先的层序遍历则需要借助队列实现。
二叉树节点定义
1
2
3
4
5
6
|
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
|
遍历的递归实现
根据定义三种遍历顺序如下:
前序遍历:根结点 —> 左子树 —> 右子树
中序遍历:左子树—> 根结点 —> 右子树
后序遍历:左子树 —> 右子树 —> 根结点
因此可以分别就定义实现二叉树的遍历:
1
2
3
4
5
6
7
|
void preorderTraversal(TreeNode* root) {
if (!root) return res;
cout<<root->val<<endl;//访问根节点
if (root->left) preorderTraversal(root->left); //遍历左子树
if (root->right) preorderTraversal(root->right); //遍历右子树
}
|
1
2
3
4
5
6
7
|
void inorderTraversal(TreeNode* root) {
if (!root) return res;
if (root->left) preorderTraversal(root->left); //遍历左子树
cout<<root->val<<endl; //访问根节点
if (root->right) preorderTraversal(root->right); //遍历右子树
}
|
1
2
3
4
5
6
7
|
void postorderTraversal(TreeNode* root) {
if (!root) return res;
if (root->left) preorderTraversal(root->left); //遍历左子树
if (root->right) preorderTraversal(root->right); //遍历右子树
cout<<root->val<<endl; //访问根节点
}
|
遍历的非递归实现
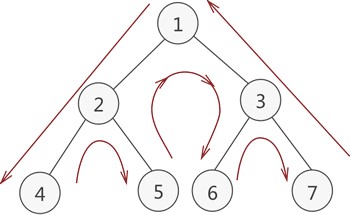
根据之前对递归版本的遍历算法分析,可以看到对于二叉树的每一个节点都访问了三次。如下图
先序遍历
因此如果在第一次访问该节点时对其遍历则就是对该二叉树的前序遍历,此时需要借助额外的数据结构栈。
前序遍历比较容易实现,可以根据定义先遍历根节点再依次遍历左子树和右子树故有以下实现方式:
根据前序遍历访问的顺序,优先访问根结点,然后再分别访问左孩子和右孩子。即对于任一结点,其可看做是根结点,因此可以直接访问,访问完之后,若其左孩子不为空,按相同规则访问它的左子树;当访问完左子树时,再访问它的右子树。因此其处理过程如下:
a. 首先申请一个新的栈,记为stack;
b. 将头根节点root压入stack中;每次从stack中弹出栈顶节点,记为p,然后打印p值,如果p右孩子不为空,则将右孩子压入栈中;
c. 如果p的左孩子不为空,将其压入stack中;
d. 重复步骤c,直到stack为空.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
void preorderTraversal(TreeNode* root) {
if (!root) return res;
stack<TreeNode*> st;
st.push(root);
while (!st.empty()){
auto p = st.top();
st.pop();
cout<<p->val<<", ";
//先压栈右节点,再压栈左节点
if (p->right) st.push(p->right);
if (p->left) st.push(p->left);
}
cout<<endl;
}
|
此外根据访问节点的顺序,在第一次访问节点时对其遍历操作,由此可以得到以下实现方式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
void preorderTraversal(TreeNode* root) {
if (!root) return;
stack<TreeNode*> st;
while (!st.empty() || root){
if (root){
cout<<root->val<<", "; //第一次访问节点
st.push(root);
root = root->left; //先访问根节点的左子树
} else {
auto p = st.top();
st.pop(); //第二次访问时将其弹出
root = p->right; //访问完左子树后访问右子树
}
}
cout<<endl;
}
|
中序遍历
根据中序遍历的顺序,对于任一结点,先访问其左孩子,而左孩子结点又可以看做一根结点,然后继续访问其左孩子结点,直到遇到左孩子结点为空的结点才进行访问,然后按相同的规则访问其右子树。也就是第一次访问节点时将其压栈,而在第二次访问时对其遍历。因此其处理过程如下:
对于给定的二叉树根节点Root
a. 若其左孩子不为空,循环将Root以及Root左子树中的所有节点的左孩子入栈;
b. 取栈顶元素p,访问p并将p出栈。然后对p的右子节点进行步骤a那样的处理;
c. 重复a和b的操作,直到p为空切栈为空。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
void inorderTraversal(TreeNode* root) {
if (!root) return;
stack<TreeNode*> st;
while (!st.empty() || root){
if (root){
st.push(root); //第一次访问时将其压栈
root = root->left; //先访问根节点的左子树
} else {
auto p = st.top();
cout<<root->val<<", "; //第二次访问节点
st.pop(); //第二次访问时将其弹出
root = p->right; //访问完左子树后访问右子树
}
}
cout<<endl;
}
|
后序遍历
后序遍历的非递归实现是三种遍历方式中最复杂的一种。因为在后序遍历中,是在第三次访问节点时对其遍历操作,而此前采用的以单个栈来存储和操作数据之多只能对每个节点访问两次。下面介绍两种方法。
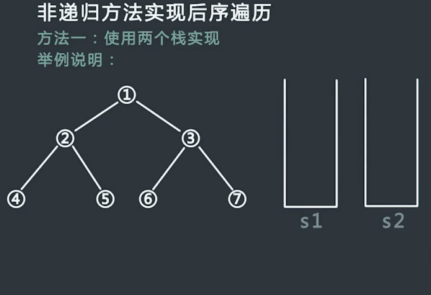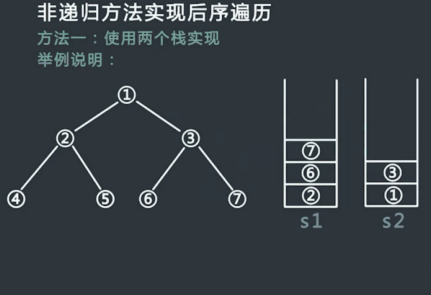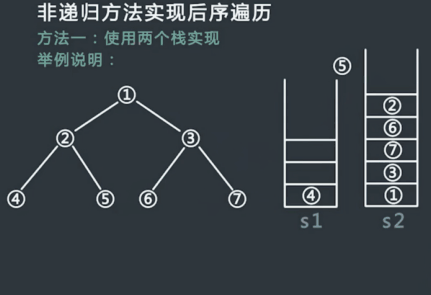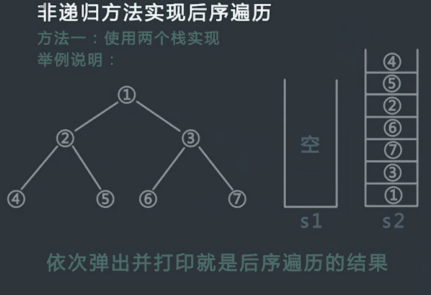
后序遍历中,我们节点的访问次序依次是:左子树 —> 右子树 —> 根结点;而前序遍历时节点访问次序依次是:根结点 —> 左子树 —> 右子树。观察可以知道前序遍历的逆序:右子树 —> 左子树 —> 根结点中只需要将左右子树的遍历顺序交换就是后序遍历的节点顺序了。因此可以借助两个辅助栈来实现该操作,第一个栈用于左右子树顺序交换的遍历,另外一个栈用于保存修正后的遍历结果并逆序输出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
void postorderTraversal(TreeNode* root) {
if (!root) return;
stack<TreeNode*> first, second;
first.push(root);
while(!first.empty()){
auto p = first.top();
first.pop();
second.push(p); //保存序列:根结点 ---> 右子树 ---> 左子树
//左子树先压栈,右子树后压栈
if (p->left) first.push(p->left);
if (p->right) first.push(p->right);
}
//逆序输出
while(!second.empty()){
cout<<second.top()->val<<", ";
second.pop();
}
cout<<endl;
}
|
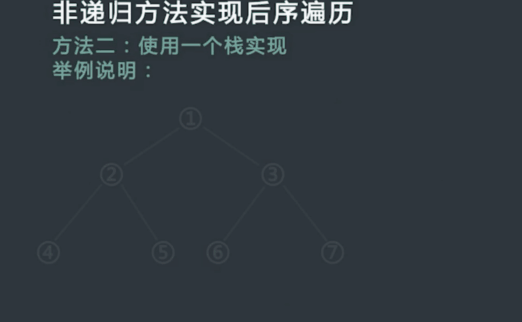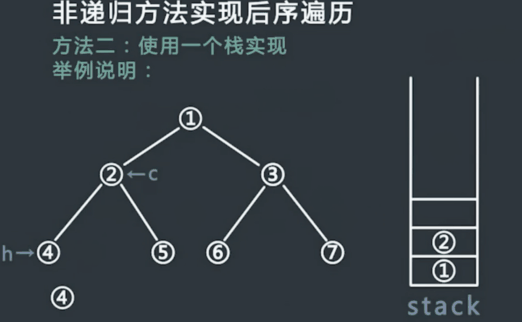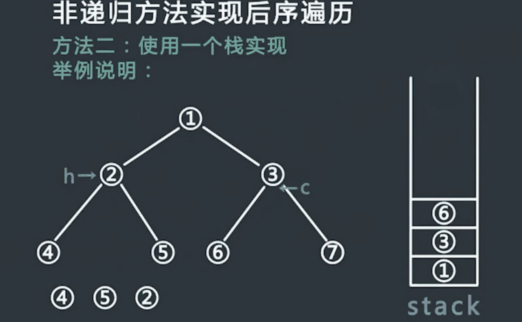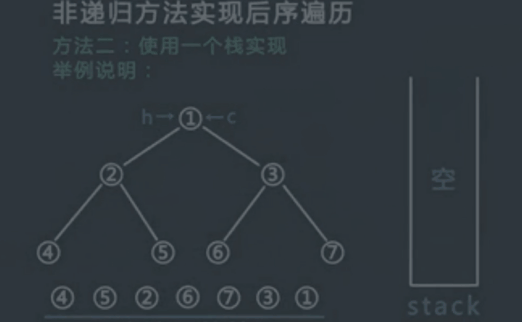
使用一个栈实现后序遍历。
a. 先将Root入栈。如果root不存在左孩子和右孩子,则可以直接访问它并出栈;
b. 如果Root存在左孩子或者右孩子,但是其左孩子和右孩子都已被访问过了,则同样可以直接访问该结点并出栈;
c. 若非上述两种情况,则将Root的右孩子和左孩子依次入栈,这样就保证了每次取栈顶元素的时候,左孩子在右孩子前面被访问,左孩子和右孩子都在父结点前面被访问。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
void postorderTraversal(TreeNode* root)
{
if (!root) return;
stack<TreeNode*> s;
TreeNode *cur; //当前结点
TreeNode *pre=NULL; //前一次访问的结点
s.push(root);
while(!s.empty())
{
cur=s.top();
if((cur->m_pLeft==NULL&&cur->m_pRight==NULL)||(pre!=NULL&&(pre==cur->m_pLeft||pre==cur->m_pRight))) //在判断当前节点时,左孩子和右孩子都在根结点前已经被访问
{
cout<<cur->val<<" "; //如果当前结点没有孩子结点或者孩子节点都已被访问过
s.pop();
pre=cur;
}
else{
if(cur->m_pRight!=NULL)
s.push(cur->m_pRight);
if(cur->m_pLeft!=NULL)
s.push(cur->m_pLeft);
}
}
cout<<endl;
}
|
层序遍历
广度优先周游的方式是按层次从上到下,从左到右的逐层访问,不难想到,可以利用一个队列来实现。基本思想是:
a. 首先把二叉树的根节点送入队列;
b. 队首的节点出队列并访问之,然后把它的右子节点和左子节点分别入队列;
c. 重复上面两步操作,直至队空。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
void levelOrderTraversal(TreeNode* root){
if(root==NULL) return;
queue<TreeNode*> queue;
queue.push(root);
while(!queue.empty()){
TreeNode* cur=queue.front();
cout<<" "<<cur->val; //visit
queue.pop();
if(cur->m_pLeft!=NULL)
queue.push(cur->m_pLeft);
if(cur->m_pRight!=NULL)
queue.push(cur->m_pRight);
}
cout<<endl;
}
|