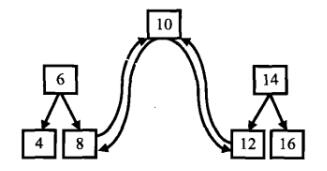
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
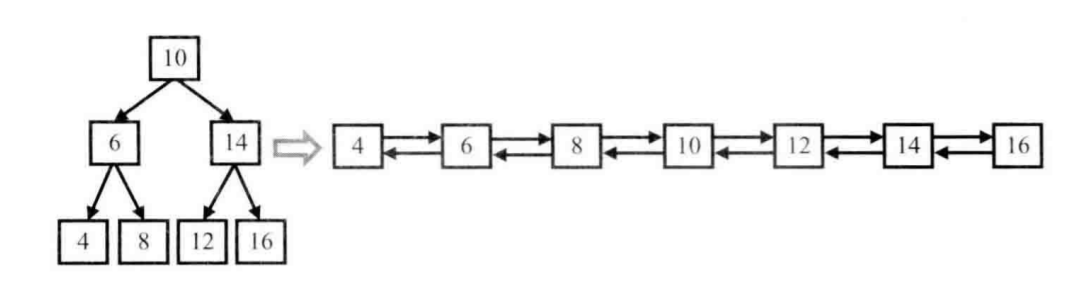
解题思路
在二叉搜索树中,左子树的值总是小于父结点的值,右子树的值总是大于父结点的值。因此我们在转换成排序双向链表时,中序遍历便是按照从小到大的顺序遍历二叉搜索树,所以我们用中序遍历树中的每一个节点得到的正好是要求的排好序的。
遍历过程如下:
每次遍历节点的左孩子、右孩子,并分别返回一个pair包含了左右子树的最左和最右叶子节点,然后把根节点的左指针指向与左子树的最右侧叶子节点,把根节点的右指针指向右子树的最左侧叶子节点,并且分别将左右子树的的这两个叶子节点的右指针和左指针指向根节点,如此递归实现。
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
TreeNode* convert(TreeNode* root) {
if (!root) return root;
pair<TreeNode*, TreeNode*> res;
res = dfs(root);
return res.first;
}
pair<TreeNode*, TreeNode*> dfs(TreeNode *root){
if (!root->left && !root->right) return {root, root};
if (root->left && root->right) {
auto leftSide = dfs(root->left);
auto rightSide = dfs(root->right);
leftSide.second->right = root;
root->left = leftSide.second;
rightSide.first->left = root;
root->right = rightSide.first;
return {leftSide.first, rightSide.second};
}
if (root->left) {
auto leftSide = dfs(root->left);
leftSide.second->right = root;
root->left = leftSide.second;
return {leftSide.first, root};
}
if (root->right) {
auto rightSide = dfs(root->right);
rightSide.first->left = root;
root->right = rightSide.first;
return {root, rightSide.second};
}
}
|